How is an uncompressed raster image laid out in computer memory? How is a pixel represented? What are stride and pitch and what do you need them for? How do you address a pixel in memory? How do you describe an image in memory?

I tried to find a web page for dummies explaining all that, and all I could find was this. So, I decided to write it down myself with the things I see as essential.

An image and a pixel

Wikipedia explains the concept of raster graphics, so let us take that idea as a given. An image, or more precisely, an uncompressed raster image, consists of a rectangular grid of pixels. An image has a width and height measured in pixels, and the total number of pixels in an image is obviouslywidth×height.

A pixel can be addressed with coordinates x,y after you have decided where the origin is and which way the coordinate axes go.

A pixel has a property called color, and it may or may not have opacity (or occupancy). Color is usually described as three numerical values, let us call them "red", "green", and "blue", or R, G, and B. If opacity (or occupancy) exists, it is usually called "alpha" or A. What R, G, B, and A actually mean is irrelevant when looking at how they are stored in memory. The relevant thing is that each of them is encoded with a certain number of bits. Each of R, G, B, and A is called a channel.

When describing how much memory a pixel takes, one can use units of bits or bytes per pixel. Both can be abbreviated as "bpp", so be careful which one it is and favour more explicit names in code. Also bits per channel is used sometimes, and channels can have a different number of bits per pixel each. For example, rgb565 format is 16 bits per pixel, 2 bytes per pixel, 5 bits per R and B channels, and 6 bits per G channel.

A pixel in memory

Pixels do not come in arbitrary sizes. A pixel is usually 32 or 16 bits, or 8 or even 1 bit. 32 and 16 bit quantities are easy and efficient to process on 32 and 64 bit CPUs. Your usual RGB-image with 8 bits per channel is most likely in memory with 32 bit pixels, the extra 8 bits per pixel are simply unused (often marked with X in pixel format names). True 24 bits per pixel formats are rarely used in memory because trading some memory for simpler and more efficient code or circuitry is almost always a net win in image processing. The term "depth" is often used to describe how many significant bits a pixel uses, to distinguish from how many bits or bytes it occupies in memory. The usual RGB-image therefore has 32 bits per pixel and a depth of 24 bits.

How channels are packed in a pixel is specified by the pixel format. There are dozens of pixel formats. When decoding a pixel format, you first have to understand if it is referring to an array of bytes (particularly used when each channel is 8 bits) or bits in a unit. A 32 bits per pixel format has a unit of 32 bits, that is uint32_t in C parlance, for instance.

The difference between an array of bytes and bits in a unit is the CPU architecture endianess. If you have two pixel formats, one written in array of bytes form and one written in bits in a unit form, and they are equivalent on big-endian architecture, then they will not be equivalent on little-endian architecture. And vice versa. This is important to remember when you are mapping one set of pixel formats to another, between OpenGL and anything else, for instance. Figure 1 shows three different pixel format definitions that produce identical binary data in memory.

Figure 1. Three equivalent pixel formats with 8 bits for each channel. The writing convention here is to list channels from highest to lowest bits in a unit. That is, abgr8888 has r in bits 0-7, g in bits 8-15, etc.

It is also possible, though extremely rare, that architecture endianess also affects the order of bits in a byte. Pixman, undoubtedly inheriting it from X11 pixel format definitions, is the only place where I have seen that.

An image in memory

The usual way to store an image in memory is to store its pixels one by one, row by row. The origin of the coordinates is chosen to be the top-left corner, so that the leftmost pixel of the topmost row has coordinates 0,0. First there are all the pixels of the first row, then the second row, and so on, including the last row. A two-dimensional image has been laid out as a one-dimensional array of pixels in memory. This is shown in Figure 2.

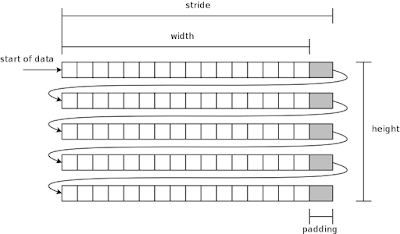Figure 2. The usual layout of pixels of an image in memory.

There are not only the width×height number of pixels, but each row also has some padding. The padding area is not used for storing anything, it only aligns the length of the row. Having padding requires a new concept: image stride.

Padding is often necessary due to hardware reasons. The more specialized and efficient hardware for pixel manipulation, the more likely it is that it has specific requirements on the row start and length alignment. For example, Pixman and therefore also Cairo (image backend particularly) require that rows are aligned to 4 byte boundaries. This makes it easier to write efficient image manipulations using vectorized or other instructions that may even process multiple pixels at the same time.

Stride or pitch

Image width is practically always measured in pixels. Stride on the other hand is related to memory addresses and therefore it is often given in bytes. Pitch is another name for the same concept as stride, but can be in different units.

You may have heard rules of thumb that stride is in bytes and pitch is in pixels, or vice versa. Stride and pitch are used interchangeably, so be sure of the conventions used in the code base you might be working on. Do not trust your instinct on bytes vs. pixels here.

Addressing a pixel

How do you compute the memory address of a given pixel x,y? The canonical formula is:

pixel_address = data_begin + y * stride_bytes + x * bytes_per_pixel.

The formula stars with the address of the first pixel in memory data_begin, then skips to row ywhile each row is stride_bytes long, and finally skips to pixel x on that row.

In C code, if we have 32 bit pixels, we can write

uint32_t *p = data_begin;
p += y * stride_bytes / sizeof(uint32_t);
p += x;

Notice, how the type of p affects the computations, counting in units of uint32_t instead of bytes.

Let us assume the pixel format in this example is argb8888 which is defined in bits of a unit form, and we want to extract the R value:

uint32_t v = *p;
uint8_t r = (v >> 16) & 0xff;

Finally, Figure 3 gives a cheat sheet.

Figure 3. How to compute the address of a pixel.

Now we have covered the essentials, and you can stop reading. The rest is just good to know.

Not everyone has the "right" way up

In the above we have assumed that the image origin is the top-left corner, and rows are stored top-most first. The most notable exception to this is the OpenGL API, which defines image data to be in bottom-most row first. (Traditionally also BMP file format does this.)

Multi-planar formats

In the above, we have talked about single-planar formats. That means that there is only a single two-dimensional array of pixels forming an image. Multi-planar formats use two or more two-dimensional arrays for forming an image.

A simple example with an RGB-image would be to store R channel in the first plane (2D-array) and GB channels in the second plane. Pixels on the first plane have only R value, while pixels on the second plane have G and B values. However, this example is not used in practice.

Common and real use cases for multi-planar images are various YUV color formats. Y channel is stored on the first plane, and UV channels are stored on the second plane, for instance. A benefit of this is that e.g. the UV plane can be sub-sampled - its resolution could be only half of the plane with Y, saving some memory.

Tiled formats

If you have read about GPUs, you may have heard of tiling or tiled formats (tiled renderer is a different thing). These are special pixel layouts, where an image is not stored row by row but a rectangular block by block. Tiled formats are far too wild and various to explain here, but if you want a taste, take a look at Nouveau's documentation on G80 surface formats.

Original post